warning Once you learn about the Reuleaux Triangle you may start to see it everwhere! In buildings, in coffee tables, in kids playground equipment, in beer logos... Reuleaux Rules Our World!

Ever wanted to drill a square-hole?

Is it possible to build a drillbit that would produce such a shape? It seems impossible, but how impossible is it? Can we drill holes that are any shape other than circular?

A circle is a curve of constant width. As you rotate a circle its width doesn't change. Does any other shape have this property?

Why yes! The Reuleaux polygons all do. The simplest and best known of which is the Reuleaux Triangle.

How do you draw a Reuleaux triangle?

Draw an equilateral triangle, and then inscribe 3 arcs, each centred on a point of the triangle and travelling between the other two points.

lt 30
repeat 3 [
fd 200
lt 120
lt 60
arc 200 60
rt 60
]

Or, draw three circles, where the centre of each circle touches the outside of the other two:

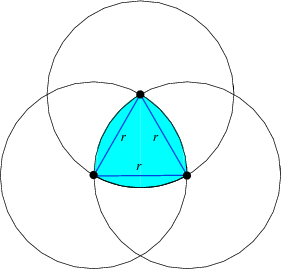
What can you do with this special shape?

You can make a drill bit that drills a square hole! (The Harry Watt square drill bit, where the drillbit needs to be mounted in a special chuck which allows for the bit not having a fixed centre of rotation)

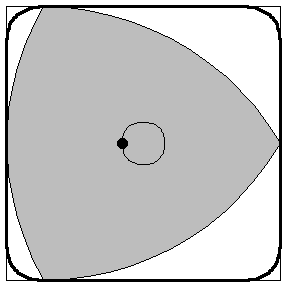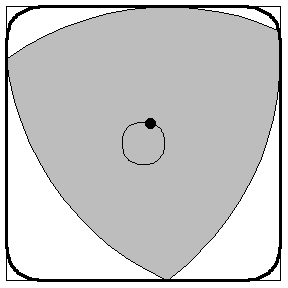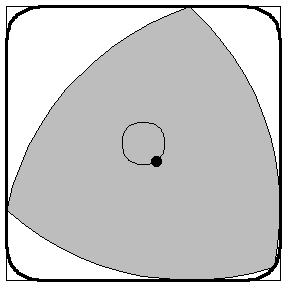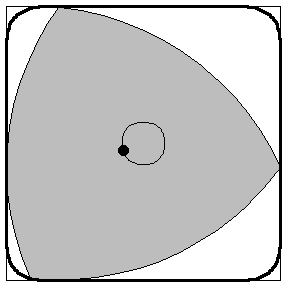
You can build rotary engines! *

You can make a bike that has ##non-circular wheels## but still gives a smooth ride.

• Regarding rotary engines:

The Wankel rotary engine isn't quite Reuleaux shaped. It says on wikipedia:

The four-stroke cycle occurs in a moving combustion chamber between the inside of an oval-like epitrochoid-shaped housing, and a rotor that is similar in shape to a Reuleaux triangle with sides that are somewhat flatter.

Here's a program for drawing multiple triangles.

to shapo :size :i :j
 repeat :i [
  rolly :size
  lt :j
 ]
end
to rolly :size
 lt 30
 repeat 3 [
   pu
   fd :size
   pd
   lt 120
   lt 60
   arc :size 60
   rt 60
 ]
 rt 30
end
shapo 150 24 15

Challenge

Can you write a program that draws a Reuleaux polygon of any number of sides?

Hint: here's a program that works only for odd-numbers of sides.

to rolly :size :sides
 repeat :sides [
   pu
   fd :size
   pd
   lt 180
   arc :size (180 / :sides)
   rt (180/ :sides)
 ]
end
rolly 150 7

External Links

• Smooth-riding Bike with Reuleaux Triangle back-wheel and Pentagonal front-wheel
• Rolling with Reuleaux
• Mathworld: Reuleaux Triangle
• Wikipedia: Reuleaux Triangle