Mathematicians: taking all the fun out of an evening stroll in Königsberg since 1735.

Only five of the famous seven bridges of Königsberg remain today.

There was a traditional puzzle, in the town of Königsberg, to try and walk around the town in such a way that you crossed each of Königsberg's bridges once and only once.

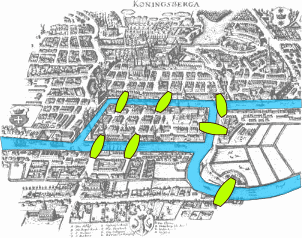
Many people had stumbled into the ale house on the central island claiming to have just concluded such a walk. But the next morning, none were ever able to reproduce their remarkable feat.

This continued for a long time until the famous mathematician Leonard Euler reluctantly agreed to put his mathematical mind to the task.

He was reluctant to start on the problem, as it was unrelated to any field of mathematics. That was no big deal for Euler though: he simply invented a new field of mathematics to which this problem belonged: graph theory.

Once he'd put on his thinking cap, squinted one eye, and set to work, he had the whole thing solved in no time.

Here's a painting of him, caught mid-thought.

Oh and he didn't simply provide a proof that no solution existed. He defined rules describing exactly what combinations of bridges and land-masses would permit a once-and-only-once traversal. He solved the more general problem to which this problem was just a specific example.

There is an XKCD cartoon that captures Euler's approach perfectly.

The first thing Euler did was to reduce the problem down to its bare essentials. The exact shape of the bridges and landmasses is irrelevant.

All that matters is that there are four landmasses. And a certain configuration of connections between them.

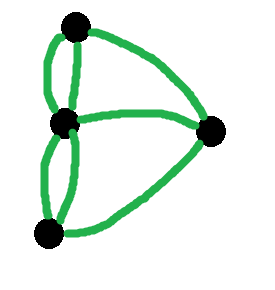
And he soon realised that the most pertinent fact was whether a landmass had an odd or even number of connections.

Let's zoom in on just one landmass:

Here we have one landmass with 3 bridges connected to it.

You can quickly deduce that if this landmass was the starting point of the journey, then it can't also be the end point of the journey. If we start here and leave by one of the bridges, then later we'll arrive by a different bridge. There will be one bridge left, and we'll have to leave by it.

Similarly, while this landmass can appear at the start or the end of the sequence (but not both), we can see that it cannot only appear in the middle of the journey.

If it was somewhere in the middle of the journey then that would mean that the visitor would arrive by one bridge, leave by another bridge, and when they next arrive at the landmass, there would be no bridges to leave by, and we would be at the end of the journey.

So, by this logic, any landmass with an odd number of connections must be visited at either the start or the end of the journey (but not both).

A journey only has 1 beginning and 1 ending. 1 + 1 = 2. Hence if there are more than two landmasses that have an odd number of connections, then there is no possible journey that would cross every bridge once and only once.

In this case we have 4 landmasses, all of which have odd numbers of bridges. 4 > 2, therefore it is not possible for every landmass to be at either the beginning or end of the walk. And thus, it's impossible to walk all 7 bridges of Königsberg once and only once.

What about the city as it stands today? Is it possible now?

Königsberg in recent times:

External Links

• A fun graph-theory activity for kids, including the 7 bridges
• Mathigon: The Bridges of Königsberg
• The most detailed article on the historical facts
• Wikipedia: Seven Bridges of Königsberg
• Wikipedia: Euler
• Explain XKCD: 974 The General Problem
• Wikipedia: The Bombing of Königsberg in World War II (wherein 2 of the bridges were destroyed)